$$\begin{array}{cc}
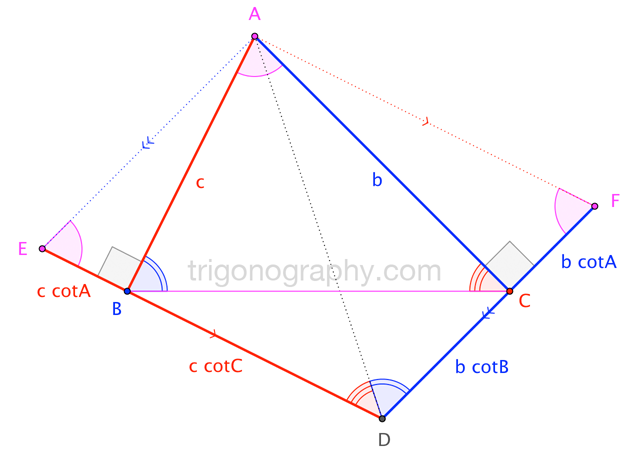
& |\overline{AC}|\,|\overline{FD}| = |AEDF| = |\overline{AB}|\,|\overline{ED}| \\[6pt]
\to \qquad & \large{b^2\,\left(\,\cot A + \cot B\,\right) = c^2\,\left(\,\cot A + \cot C\,\right)} \\
\end{array}$$
Cotangent Identity
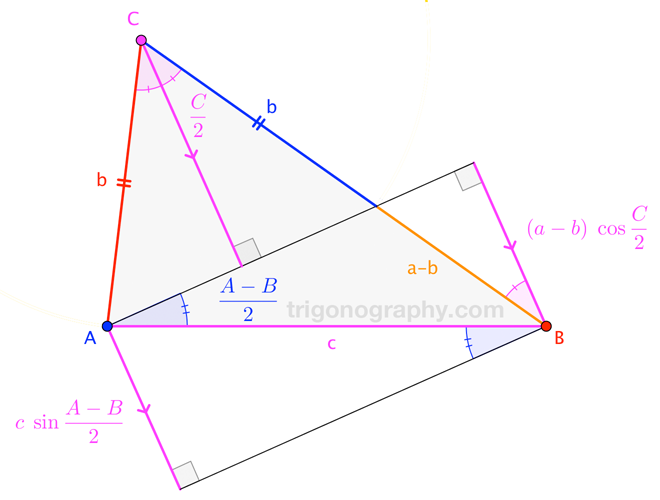
Half-Angles in a Triangle
My answer to this question at Math.StackExchange.com.
$$\Large{c\;\sin\frac{A-B}{2} \;\equiv\; (a-b)\;\cos\frac{C}{2}}$$
Identity from Math.StackExchange.com
Taken from my answer to “Proving a weird trig identity” at Math.StackExchange.com .
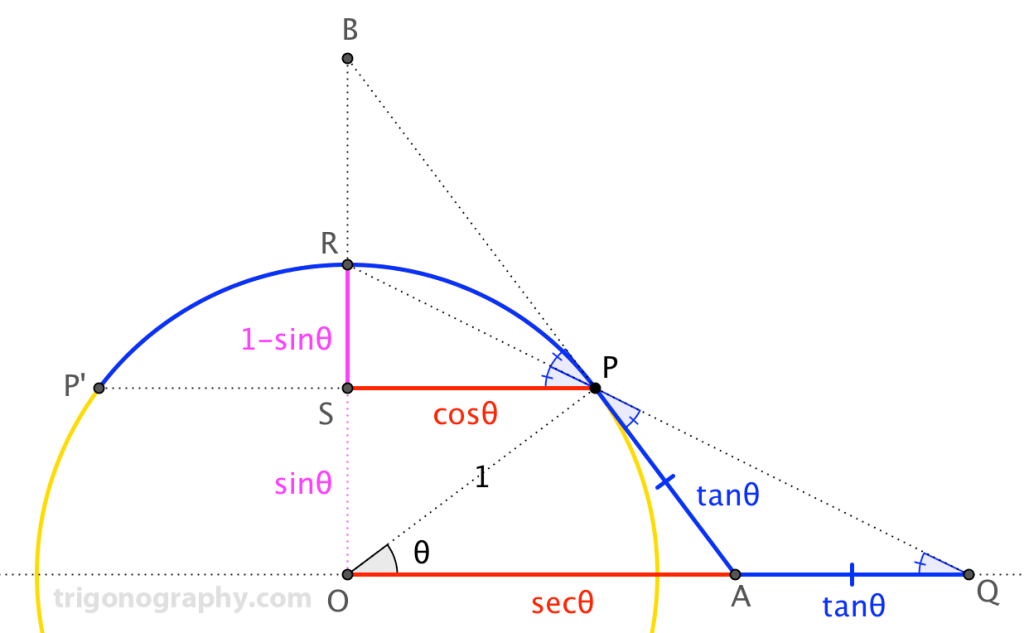
$$\Large{\frac{\cos\theta}{1-\sin\theta} = \frac{\sec\theta + \tan\theta}{1}}$$
In the diagram, \(\overline{AB}\) is tangent to the unit circle at P. The “trig lengths” (except for \(|\overline{AQ}|\)) should be clear.
We note that \(\angle BPR \cong \angle RPP^\prime\), since these inscribed angles subtend congruent arcs \(\stackrel{\frown}{PR}\) and \(\stackrel{\frown}{RP^\prime}\). Very little angle chasing gives that \(\triangle APQ\) is isosceles, with \(\overline{AP}\cong \overline{AQ}\) (justifying that last trig length). Then,
$$\triangle SPR \sim \triangle OQR \Longrightarrow \frac{|\overline{SP}|}{|\overline{SR}|}=\frac{|\overline{OQ}|}{|\overline{OR}|}\Longrightarrow \frac{\cos\theta}{1−\sin\theta}=\frac{\sec\theta+\tan\theta}{1}$$
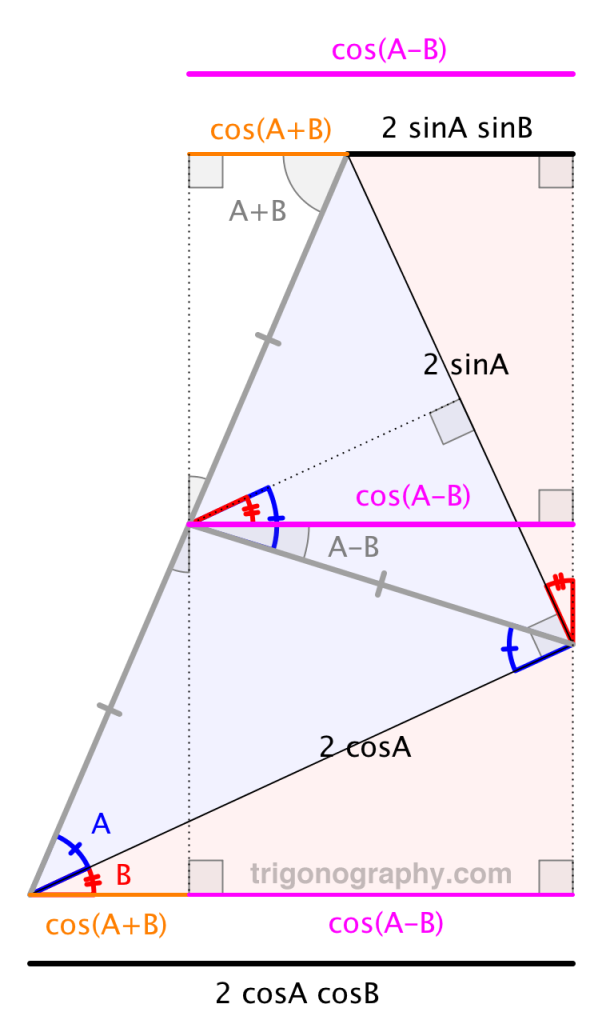
Product Identities
$$\begin{align}
2 \cos A \cos B &= \cos(A-B) \;+\; \cos(A+B) \\
2 \sin A \;\sin B &= \cos(A-B) \;-\; \cos(A+B)
\end{align}$$
Proof without words: Pi from Square(root)s
$$ \huge \sqrt{2} + \sqrt{3} \;\approx\; \pi $$
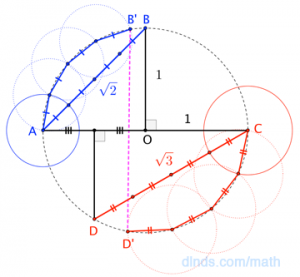
$$\large \begin{align}
\sqrt{2} + \sqrt{3} &= |\overline{AB}| + |\overline{CD}| \\
&= |\widehat{AB^\prime}| + |\widehat{CD^\prime}| \\
&\approx |\stackrel{\frown}{AB^\prime}| + |\stackrel{\frown}{CD^\prime}| \\
&\approx |\stackrel{\frown}{AC}| \\[6pt]
&= \pi
\end{align}$$