The hedronometric (“area-based”) Pythagorean Theorem for Right-Corner Tetrahedra generalizes to an unsurprising Law of Cosines:
\(\displaystyle{W^2 = X^2 + Y^2 + Z^2 – 2 Y Z \cos DA – 2 Z X \cos DB – 2 X Y \cos DC}\)
for face areas \(W\), \(X\), \(Y\), \(Z\) and dihedral angles \(DA\), \(DB\), \(DC\). I recently learned (while browsing Boyer’s A History of Mathematics at a Barnes & Noble) that, as early as 1803, the mathematician Carnot was aware of this result —which beats me by about 180 years— but I’m not yet sure who else may have been aware of this variation:
\(\displaystyle{W^2 + X^2 – 2 W X \cos BC = Y^2 + Z^2 – 2 Y Z \cos DA}\)
or who else, better still, may have thought the above looked too much like the trigonometric Law of Cosines not to introduce an element, say \(H\), such that
\(\displaystyle{W^2 + X^2 – 2 W X \cos BC = H^2 = Y^2 + Z^2 – 2 Y Z \cos DA}\)
For early TeX practice in 2005, I transcribed some old journal notes recognizing \(H\) as not just an algebraic imperative but a legitimate geometric aspect of a tetrahedron, and I dubbed the thing a “pseudoface”. While my notes —“Pseudofaces of Tetrahedra”— are somewhat clumsy and haphazard, subsequent research has indicated that this pseudoface idea actually constitutes a pretty interesting part of tetrahedral lore. I explore that lore in later papers … with (I like to think) increasingly-improved prose and TeX-ification.
Barlotti’s Theorem states that an “affinely regular” polygon is the vertex sum of two regular polygons of the same type. This result can be interpreted as a straightforward decomposition of 2×2 matrices, which in turn can be extended to a decomposition of dxd matrices, which immediately gives rise to the (Extended) Barlotti Theorem for Multiple Dimensions.
My paper —aptly entitled “An Extension of a Theorem of Barlotti to Multiple Dimensions”— discusses generalizing the notion of vertex sum to “point sum”, so that the Extended Barlotti provides such statements as any ellipsoid is the point sum of three spheres.
The Extended Barlotti Theorem implies that spectral realizations of a graph (see this post) form an additive basis of all realizations of that graph; that is, any realization can be expressed as the vertex sum of (harmonious) spectral realizations.
“Spectral realizations” of a (combinatorial) graph have two important properties: they are harmonious (each graph automorphism induces a rigid symmetry) and eigenic (replacing each vertex with the vector sum of its neighbors yields the same result as scaling the figure).
My paper “Spectral Realizations of Graphs” describes a straightforward way of generating the spectral realizations of any graph, using basic eigen-analysis of the graph’s adjacency matrix. (Interestingly, while there’s such a thing as spectral graph theory for the study of graph properties via adjacency matrix properties, this particular avenue seems not to have been explored.) The paper also begins the process of cataloging the hundreds of realizations of the uniform polyhedra and their duals. (I really need to construct a proper database of this material.) A future paper will describe how these realizations makes up an additive basis of all realizations of a graph.
The Open Question in this:
Is there a nice, mechanical way to generate “good” coordinates for various realizations?
For the figures in the paper, I simply had Mathematica churn out various orthonormal bases for things, and compute coordinates from those, which gives the realizations somewhat random orientations. I don’t doubt that I’m missing-out on some key appearances by the golden ratio and such.
When you (like I) think that the trig functions are best understood as segments within the Complete Triangle, you tend to believe that just about every important fact about those functions has a nifty geometric interpretation. (See other posts in this category.)
Why shouldn’t we expect this to be true of the functions’ power series?
(Maybe because taking powers of angles isn’t the most intuitive process?)
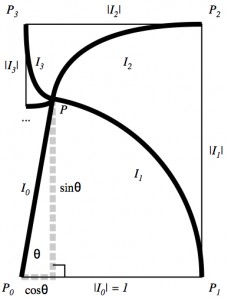
As it turns out, mathematician (and teacher) Y. S. Chaikovsky elegantly illustrated the power series for sine and cosine as a kind of pinwheel of involutes (first the involute of the circular arc, then the involute of that involute, then the involute of that involute, and so on).
In the diagram, the thick curves, \(I_i\), are the successive involutes. (We include the radius segment as \(I_0\) and the circular arc as \(I_1\) for symbolic completeness.) The nature of involutes is that they trace the path of “unrolling” a curve, which effectively transfers the lengths of the curves in the involute pinwheel onto the sides of the polygonal spiral. As the corners of that spiral —\(P_0, P_1, P_2, P_3, \dots\)— close in on the tip of the inclined radius segment, alternately over- and under-shooting the mark both horizontally and vertically, we see
\(\displaystyle{\begin{align}
\cos\theta &= |I_0| – |I_2| + |I_4| – \cdots = \sum (-1)^i |I_{2i}| \\
\sin\theta &= |I_1| – |I_3| + |I_5| – \cdots = \sum (-1)^i |I_{2i+1}|
\end{align}}\)
A little combinatorics, and an appeal to a basic Calculus result —namely, \(\lim_{x\to 0} \frac{\sin x}{x} = 1\)— help Chaikovsky show that the lengths of successive involutes depict powers of the angle (that is, powers of the length of the circular arc) —\(|I_i| = \frac{1}{i!}\theta^i\)— so that we have our power series
\(\displaystyle{
\cos\theta = \sum (-1)^i \frac{\theta^{2i}}{(2i)!} \qquad \sin\theta = \sum (-1)^i \frac{\theta^{2i+1}}{(2i+1)!}}\)
A nifty geometric interpretation, indeed!
With a very-minor conceptual tweak (along with some more-intense combinatorial analysis), I was able to adapt Chaikovsky’s involute pinwheel into an involute zig-zag illustrating the series for secant and tangent (in their natural habitat as segments of the Complete Triangle!):
A full discussion is here: “Zig-Zag Involutes, Up-Down Permutations, and Secant and Tangent”.
The Open Question in this:
What about Cosecant and Cotangent?
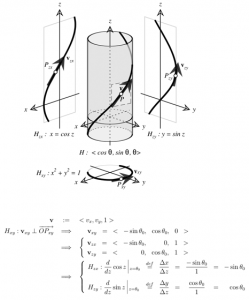
I’d like to think that the following constitutes a Proof without Words of the formulas for the derivatives of sine and cosine.
Unfortunately, it seems that words may be in order, so I wrote some here: “Calculus-free Derivatives of Sine and Cosine” … even though, strictly speaking, the proof isn’t entirely calculus-free. (Why we expect the projection of the tangent line to a helix to be tangent to the planar projections of the helix needs justification.)
But the idea is good for the intuition.
I even made an interactive illustration for the Wolfram Demonstrations Project.